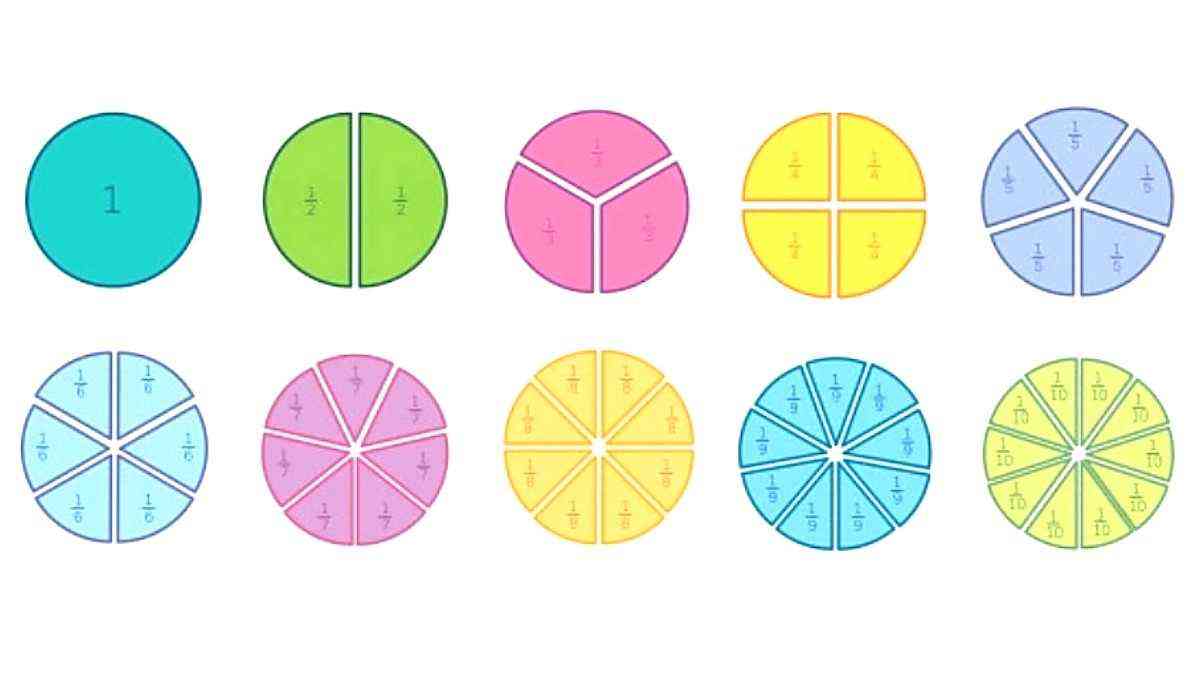
perbandingan pecahan – Pernah merasa kesulitan untuk memahami atau mengajarkan materi pecahan kepada adik atau saudara terdekat?
Sederhananya, pecahan adalah bilangan yang menyatakan bagian dari keseluruhan. Selain memahami pengertiannya, apakah kamu mengetahui bagaimana cara menentukan pecahan mana yang lebih kecil atau besar? Di sinilah letak pentingnya konsep perbandingan pecahan yang dipelajari di tingkat Sekolah Dasar. Selain menjadi sebuah operasi matematika, konsep ini juga sangat berguna dalam kehidupan kita sehari-hari.
Selain mengetahui konsep dasarnya, Gramin juga akan menyertakan beberapa contoh soal perbandingan pecahan–lengkap dengan cara menghitungnya. Yuk, baca artikel ini hingga selesai!
Tingkatkan keterampilan berhitungmu dengan buku yang menyenangkan ini. Aktivitas dalam buku ini akan membantu membangun keyakinan dan percaya dirimu akan konsep berhitung utama seperti pecahan, desimal, dan persen. Dengan mengerjakan latihan dalam buku ini, kalian akan menguasai keterampilan baru, mengatasi soal bilangan, dan meningkatkan pembelajaran di sekolah.
Desimal merupakan salah satu cara atau cara lain menuliskan pecahan baik pecahan biasa maupun pecahan campuran. Desimal adalah bilangan yang dinyatakan dalam skala puluhan. Secara umum kita berbicara tentang desimal ketika bilangan menyertakan titik desimal untuk mewakili seluruh bilangan ditambah sebagian kecil dari seluruh nilai sebuah bilangan (sepersepuluh, ratusan, dll). Titik desimal adalah titik yang digunakan untuk memisahkan bilangan cacah dengan sebuah pecahan (nilai lebih kecil dari 1).
Daftar isi :
Memahami pecahan
Pecahan setara
Menghitung dalam pecahan
Mengurutkan pecahan satuan
Mengurutkan pecahan bukan satuan
Mengurutkan pecahan setara
Menjumlahkan pecahan
Mengurangi pecahan
Memahami persepuluhan
Persepuluhan dalam desimal
Mengurutkan desimal
Memahami perseratusan
Pecahan dan desimal setara
Menjumlahkan pecahan dan desimal
Menjumlahkan satuan dan desimal
Membagi satuan dengan 10
Membagi satuan dengan 100
Membulatkan
Mengurutkan desimal
Membandingkan desimal
Menjumlahkan desimal
Penghitungan pecahan
Penghitungan desimal
Pecahan tak wajar
Mengubah pecahan dan desimal
Mengurutkan pecahan dan desimal
Mengenalkan persentase
Daftar Isi
Apa Itu Perbandingan Pecahan?
Perbandingan pecahan adalah cara untuk membandingkan dua pecahan atau lebih untuk menentukan mana yang lebih besar, lebih kecil, atau keduanya sama.
Misalnya saja, pecahan 12 artinya satu bagian dari dua bagian yang sama besar. Dalam perbandingan ini, kamu bisa menggunakan berbagai cara–seperti menyamakan penyebut, mengubah ke bentuk desimal, atau melihat bentuk visual.
Perbandingan pecahan ini penting dipelajari karena sering digunakan dalam kehidupan sehari-hari. Misalnya saat membagi makanan, mengatur waktu, atau memahami resep. Untuk anak kelas 3 SD, konsep ini menjadi dasar penting sebelum belajar pecahan lebih lanjut di jenjang berikutnya.
Cara Menghitung Perbandingan Pecahan
Berikut adalah cara untuk menghitung perbandingan pecahan langkah demi langkah yang dapat Grameds ikuti:
Langkah 1: Perhatikan Penyebut Pecahan
Jika kedua pecahan yang akan dibandingkan memiliki penyebut yang sama, kamu bisa langsung membandingkan pembilangnya. Pecahan dengan pembilang lebih besar artinya nilai pecahan tersebut lebih besar.
Jika kedua pecahan memiliki penyebut yang berbeda, kamu harus menyamakan penyebutnya terlebih dahulu agar bisa dibandingkan dengan tepat.
Langkah 2: Menyamakan Penyebut (Jika Berbeda)
Cari Kelipatan Persekutuan Terkecil (KPK) dari kedua penyebut pecahan tersebut.
Contohnya, jika kamu ingin membandingkan 35 dan 68 maka KPK dari 5 dan 8 adalah 40.
Ubahlah kedua pecahan tersebut menjadi pecahan dengan penyebut KPK tadi dengan cara mengalikan pembilang (angka yang berada di bagian atas garis) dan penyebut (angka yang berada di bagian bawah garis) setiap pecahan dengan bilangan yang membuat penyebutnya menjadi KPK.
Misalnya:
35=35x 88 =2440
68=68x 55 =3040
Langkah 3: Bandingkan Pembilang Pecahan yang Sudah Sama Penyebutnya
Setelah penyebut sama, kamu bisa langsung membandingkan penyebutnya. Jika kita lihat contoh di atas, bilangan 30 jauh lebih besar dibandingkan 24.
Pecahan dengan pembilang lebih besar adalah pecahan yang nilainya lebih besar. Jika pembilang sama, maka kedua pecahan tersebut sama nilainya. Hasilnya, pecahan 35 lebih kecil dibandingkan 68.
Buku ini dipersiapkan pemerintah dalam rangka implementasi Kurikulum 2013. Buku siswa ini disusun dan ditelaah oleh berbagai pihak di bawah koordinasi Kementerian Pendidikan dan Kebudayaan dan dipergunakan dalam tahap awal penerapan Kurikulum 2013. Buku ini merupakan “dokumen hidup” yang senantiasa diperbaiki, diperbaharui, dan dimutakhirkan sesuai dengan dinamika kebutuhan dan perubahan zaman.
Matematika merupakan mata pelajaran wajib di tingkat dasar hingga menengah. Hal tersebut sudah berlaku karena terdapat di dalam kurikulum yang dibuat oleh dinas terkait. Tidak sedikit dari murid yang mengaku tidak suka dengan pelajaran ini dengan berbagai alasan, mulai dari membosankan, guru yang killer, dsb.
Buku Pintar Matematika SD Kelas 3 Kurikulum 2013 ini disusun untuk mempermudah siswa tingkat Sekolah Dasar (SD) kelas 3 dalam memahami materi pelajaran matematika yang diberikan guru di sekolah. Buku ini disusun secara praktis dan sistematis berdasarkan ketentuan dan pedoman kurikulum 2013. Buku ini dilengkapi dengan ringkasan materi dan contoh soal dan pembahasan, sehingga siswa akan lebih mudah untuk memahami cara menyelesaikan model soal matematika. Selain itu, dalam buku ini juga terdapat latihan soal ulangan harian, umum, dan ujian semester. Sehingga siswa dapat berlatih persiapan sebelum ujian. Buku ini bermanfaat sebagai salah satu wahana dalam penguasaan kompetensi pembentukan kemandirian dan belajar aktif, namun tetap diperlukan guru dalam mengembangkan dan melaksanakan kurikulum ini.
Contoh Soal Perbandingan Pecahan
Untuk menguji pemahamanmu, berikut Gramin sertakan 30 soal perbandingan pecahan yang dapat dikerjakan. Pastikan untuk mengerjakannya semampumu dahulu sebelum mengecek pembahasannya!
Soal 1–10: Bandingkan Pecahan Langsung
1. Mana yang lebih besar: ⅔ atau ¾?
Jawaban: ¾
Penjelasan: Kalau kamu ubah kedua pecahan ke penyebut yang sama, misalnya 12, maka ⅔ jadi 8/12 dan ¾ jadi 9/12. Karena 9/12 lebih besar dari 8/12, maka ¾ lebih besar dari ⅔.
2. Bandingkan: ½ ___ ⅓
Jawaban: ½ > ⅓
Penjelasan: Setengah berarti satu bagian dari dua, sementara sepertiga berarti satu dari tiga bagian. Karena dua bagian lebih besar dari tiga, maka ½ lebih besar dari ⅓.
3. Mana yang lebih kecil: ⅖ atau ⅗?
Jawaban: ⅖
Penjelasan: Kedua pecahan ini punya penyebut yang sama, yaitu lima. Tapi ⅖ hanya punya dua bagian dari lima, sedangkan ⅗ punya tiga. Jadi ⅖ lebih kecil dari ⅗.
4. Apakah ¼ lebih besar dari ⅛?
Jawaban: Ya
Penjelasan: ¼ berarti satu bagian dari empat, sedangkan ⅛ adalah satu bagian dari delapan. Semakin banyak bagian, semakin kecil ukuran tiap bagiannya. Jadi ¼ lebih besar.
5. Bandingkan: ⅚ ___ ⅞
Jawaban: ⅞ > ⅚
Penjelasan: Walaupun keduanya besar, ⅞ memiliki bagian lebih banyak dari delapan dibandingkan dengan ⅚ yang hanya enam bagian dari enam. Jika disamakan penyebutnya, ⅞ tetap lebih besar.
6. Apakah ⅘ = ⁸⁄₁₀?
Jawaban: Ya
Penjelasan: Kalau kamu kalikan pembilang dan penyebut dari ⅘ dengan 2, hasilnya adalah ⁸⁄₁₀. Artinya, nilai kedua pecahan ini sama besar.
7. Manakah lebih besar: ⁴⁄₆ atau ⅔?
Jawaban: Sama
Penjelasan: Pecahan ⁴⁄₆ bisa disederhanakan jadi ⅔ karena 4 dan 6 sama-sama bisa dibagi 2. Jadi keduanya punya nilai yang sama.
8. Apakah ⅜ lebih kecil dari ½?
Jawaban: Ya
Penjelasan: Bayangkan satu batang cokelat dibagi 8, dan kamu ambil 3 bagian. Itu lebih sedikit dari setengah batang, jadi ⅜ lebih kecil dari ½.
9. Manakah yang lebih besar: ⅝ atau ⅗?
Jawaban: ⅝
Penjelasan: Dalam bentuk desimal, ⅝ adalah 0,625 sedangkan ⅗ adalah 0,6. Karena 0,625 > 0,6 maka ⅝ lebih besar.
10. Bandingkan: ⅖ ___ ⅘
Jawaban: ⅖ < ⅘
Penjelasan: Kedua pecahan memiliki penyebut yang sama yaitu 5. Karena 4 lebih besar dari 2, maka ⅘ lebih besar dari ⅖.
Bagi sebagian orang pelajaran matematika itu menyulitkan. Nah, menurutmu menyulitkan tidak? Dengan metode belajar yang tepat dan menyenangkan, matematika bisa dibuat mudah, lho. Menguasai matematika memiliki banyak keuntungan. Harus disadari bahwa matematika bermanfaat untuk menunjang kehidupan sehari-hari. Minimal kita tidak perlu menggunakan kalkulator.
Buang jauh-jauh pikiran kalau matematika itu sulit. Penting untuk mengubah mindset dan meyakinkan diri sendiri bahwa matematika itu tidak rumit dan bisa dipahami. Sugesti yang positif tentunya bisa bikin lebih termotivasi untuk belajar matematika dan tidak gampang menyerah kalau menemukan materi yang sulit. Ingat juga kalau matematika dibutuhkan buat hidup sehari-hari, sehingga matematika pun butuh dipelajari.
Buat catatan rumus dengan rapi dalam buku catatan favorit. Ada studi yang menyatakan kalau mencatat dapat melatih daya ingat, karena adanya proses mengolah materi yang diterima menjadi catatan dalam bahasa kita sendiri. Selain itu, proses belajar yang dilalui pasti lebih efektif karena tidak perlu bolak-balik halaman buku materi hanya untuk cari satu baris rumus.
“Buku Pintar Rumus-Rumus Matematika SD” ini berisikan kumpulan rumus-rumus matematika lengkap dipadu dengan penjelasan dan contoh soal disertai dengan penyelesaiannya. Dengan menggunakan metode penyajian materi yang sistematis, ringkas, jelas, dan mudah dipahami buku ini akan dapat membantu para siswa sekolah dasar dalam memahami dan menguasai pelajaran Matematika secara cepat dan tepat.
Soal 11–20: Gunakan Penyebut Sama
11. Bandingkan: ¾ dan ⅚
Jawaban: ⅚
Penjelasan: ¾ setara dengan 9/12, dan ⅚ setara dengan 10/12. Karena 10 lebih besar dari 9, maka ⅚ lebih besar.
12. Apakah ⅞ lebih besar dari ⅝?
Jawaban: Ya
Penjelasan: Pecahan dengan penyebut sama bisa dibandingkan dengan pembilang. Karena 7 lebih besar dari 5, maka ⅞ > ⅝.
13. Bandingkan: ¾ ___ ⅗
Jawaban: ¾ lebih besar
Penjelasan: Ubah ke penyebut 20 → ¾ = 15/20 dan ⅗ = 12/20. Maka 15 > 12.
14. Apakah ⁶⁄₁₀ dan ⅗ setara?
Jawaban: Ya
Penjelasan: Pecahan ⁶⁄₁₀ bisa disederhanakan dengan dibagi 2, hasilnya ⅗.
15. Bandingkan: ⅜ dan ⁶⁄₁₆
Jawaban: ⅜ lebih besar
Penjelasan: ⅜ = 0,375 sedangkan ⁶⁄₁₆ = 0,375. Ternyata keduanya sama besar.
16. Mana lebih kecil: ⅓ atau ⅖?
Jawaban: ⅓
Penjelasan: Dalam bentuk desimal, ⅓ = 0,33 dan ⅖ = 0,4. Maka ⅓ lebih kecil.
17. Bandingkan: ⅚ dan ¾
Jawaban: ⅚
Penjelasan: Karena 5/6 = 0,83 dan ¾ = 0,75, maka ⅚ lebih besar.
18. Apakah ⅗ = ⁹⁄₁₅?
Jawaban: Ya
Penjelasan: Jika ⅗ dikalikan 3, hasilnya ⁹⁄₁₅.
19. Manakah yang lebih besar: ⁵⁄₆ atau ¹⁰⁄₁₂?
Jawaban: Sama
Penjelasan: ⁵⁄₆ jika dikali 2 menjadi 10/12, jadi nilainya sama besar.
20. Bandingkan: ¾ dan ⁶⁄₈
Jawaban: Sama
Penjelasan: ¾ dikali 2 = 6/8. Jadi keduanya sama.
Soal 21–30: Cerita dan Aplikasi
21. Budi makan ½ bagian kue, Sari makan ¾. Siapa makan lebih banyak?
Jawaban: Sari
Penjelasan: ¾ lebih besar dari ½, jadi Sari makan lebih banyak.
22. Dina punya pita ⅔ meter, Nia punya ⅚ meter. Siapa lebih panjang?
Jawaban: Nia
Penjelasan: ⅚ > ⅔, jadi pita Nia lebih panjang.
23. Dalam sebuah grafik, warna merah ⅓ dan biru ¼. Warna mana lebih besar?
Jawaban: Merah
Penjelasan: ⅓ = 0.33 dan ¼ = 0.25.
24. Ibu memberi Rina ⅘ roti dan Nina ⅗. Siapa lebih banyak?
Jawaban: Rina
Penjelasan: ⅘ lebih besar dari ⅗ karena 4 > 3 dengan penyebut sama.
25. ¾ siswa suka Matematika, ⅝ suka IPA. Mana yang lebih banyak?
Jawaban: Matematika
Penjelasan: ¾ = 0.75, ⅝ = 0.625.
26. Ani menjawab ⅔ soal, Budi ¾ soal. Siapa lebih banyak?
Jawaban: Budi
Penjelasan: Karena ¾ > ⅔.
27. ⁷⁄₈ kue dimakan pagi, ⁵⁄₈ malam. Kapan lebih banyak?
Jawaban: Pagi
Penjelasan: Karena 7 > 5.
28. Rina baca ⅗ buku, Lani ⅖ buku. Siapa lebih banyak?
Jawaban: Rina
Penjelasan: ⅗ > ⅖.
29. ⅝ siswa bawa bekal, ¾ tidak. Mana lebih banyak?
Jawaban: Yang tidak bawa bekal
Penjelasan: Karena ¾ = 0.75 dan ⅝ = 0.625.
30. Ayah potong kayu ⁹⁄₁₀ meter, Ibu ⁷⁄₁₀ meter. Siapa lebih panjang?
Jawaban: Ayah
Penjelasan: ⁹⁄₁₀ = 0.9, sedangkan ⁷⁄₁₀ = 0.7. Jadi ayah memotong lebih panjang.
Belajar Matematika Jadi Lebih Menyenangkan bersama Gramedia!
Melalui artikel ini, sekarang kamu sudah mengetahui apa itu perbandingan pecahan, cara menghitungnya, dan mengikuti 30 contoh soalnya yang cocok untuk kelas 3 SD. Giatlah untuk berlatih dengan soal-soal lainnya supaya bisa lebih percaya diri saat mengajarkannya kepada adik atau mengerjakan ujian sekolah!
Kalau kamu tertarik untuk mempelajari materi pecahan lebih lanjut, Gramedia punya buku-buku menarik yang relevan dengan kebutuhan pembelajaran Matematika tingkat Sekolah Dasar–termasuk pecahan.
Di sini, kamu bisa menemukan materi yang super lengkap hingga kumpulan soal yang dapat dikerjakan untuk menambah pengetahuanmu di bidang ini.
Jadikan pembelajaranmu lebih menarik lagi dengan buku yang tepat! Yuk, kunjungi halaman Gramedia.com dan dapatkan buku-buku favorit incaranmu!